最短路径算法--弗洛伊德算法

在一个加权图中，如果想找到各个顶点之间的最短路径，可以考虑使用弗洛伊德算法。

弗洛伊德算法既适用于无向加权图，也适用于有向加权图。使用弗洛伊德算法查找最短路径时，只允许环路的权值为负数，其它路径的权值必须为非负数，否则算法执行过程会出错。

弗洛伊德算法的实现思路

弗洛伊德算法是基于动态规划算法实现的，接下来我们以在图 1 所示的有向加权图中查找各个顶点之间的最短路径为例，讲解弗洛伊德算法的实现思路。

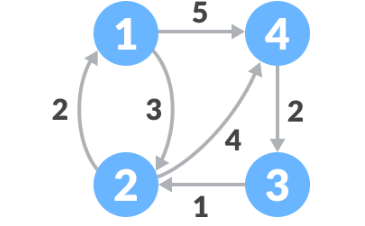
弗洛伊德算法查找图 1 中各个顶点之间的最短路径，实现过程如下：

1. 建立一张表格，记录每个顶点直达其它所有顶点的权值：
   

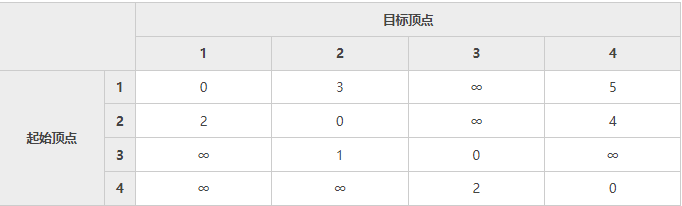
2. 在表 1 的基础上，将顶点 1 作为 "中间顶点"，计算从各个顶点出发途径顶点 1 再到达其它顶点的权值，如果比表 1 中记录的权值更小，证明两个顶点之间存在更短的路径，对表 1 进行更新。

从各个顶点出发，途径顶点 1 再到达其它顶点的路径以及对应的权值分别是：
2-1-3：权值为 2 + ∞ = ∞，表 1 中记录的 2-3 的权值也是 ∞；
2-1-4：权值为 2 + 5 = 7，表 1 中记录的 2-4 的权值是 4；
3-1-2：权值为 ∞ + 3，表 1 中记录的 3-2 的权值是 1；
3-1-4：权值为 ∞ + 5，表 1 中记录的 3-4 的权值是 ∞；
4-1-2：权值为 ∞ + 3，表 1 中记录的 4-2 的权值是 ∞；
4-1-3：权值为 ∞ + ∞，表 1 中记录的 4-3 的权值是 2。

以上所有的路径中，没有比表 1 中记录的权值最小的路径，所以不需要对表 1 进行更新。

3. 在表 1 的基础上，以顶点 2 作为 "中间顶点"，计算从各个顶点出发途径顶点 2 再到达其它顶点的权值：
   1-2-3：权值为 3 + ∞，表 1 中记录的 1-3 的权值为 ∞；
   1-2-4：权值为 3 + 4 = 7，表 1 中 1-4 的权值为 5；
   3-2-1：权值为 1 + 2 = 3，表 1 中 3-1 的权值为 ∞，3 < ∞；
   3-2-4：权值为 1 + 4 = 5，表 1 中 3-4 的权值为 ∞，5 < ∞；
   4-2-1：权值为 ∞ + 2，表 1 中 4-1 的权值为 ∞；
   4-2-3：权值为 ∞ + ∞，表 1 中 4-3 的权值为 2。

以顶点 2 作为 "中间顶点"，我们找到了比 3-1、3-4 更短的路径，对表 1 进行更新：

4. 在表 2 的基础上，将顶点 3 作为 "中间顶点"，计算从各个顶点出发途径顶点 3 再到达其它顶点的权值：
   1-3-2 权值为 ∞ + 1，表 2 中 1-2 的权值为 3；
   1-3-4 权值为 ∞ + 5，表 2 中 1-4 的权值为 5；
   2-3-1 权值为 ∞ + 3，表 2 中 2-1 的权值为 2；
   2-3-4 权值为 ∞ + 5，表 2 中 2-4 的权值为 4；
   4-3-1 权值为 2 + 3 = 5，表 2 中 4-1 的权值为 ∞，5 < ∞；
   4-3-2 权值为 2 + 1 = 3，表 2 中 4-2 的权值为 ∞，3 < ∞；

以顶点 3 作为 "中间顶点"，我们找到了比 4-1、4-2 更短的路径，对表 2 进行更新：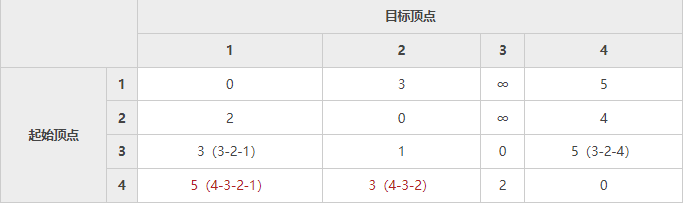

5. 在表 3 的基础上，将顶点 4 作为 "中间顶点"，计算从各个顶点出发途径顶点 4 再到达其它顶点的权值：
   1-4-2 权值为 5 + 3 = 8，表 3 中 1-2 的权值为 3；
   1-4-3 权值为 5 + 2 = 7，表 3 中 1-3 的权值为 ∞，7 < ∞；
   2-4-1 权值为 4 + 5 = 9，表 3 中 2-1 的权值为 2；
   2-4-3 权值为 4 + 2 = 6，表 3 中 2-3 的权值为 ∞，6 < ∞；
   3-4-1 权值为 4 + 5 = 9，表 3 中 3-1 的权值为 3；
   3-4-2 权值为 5 + 5 = 10 ，表 3 中 3-2 的权值为 1。

以顶点 4 作为 "中间顶点"，我们找到了比 1-3、2-3 更短的路径，对表 3 进行更新：

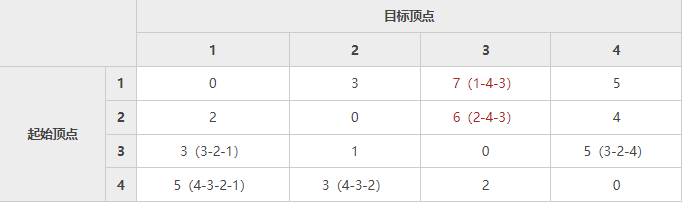
通过将所有的顶点分别作为“中间顶点”，最终得到的表 4 就记录了各个顶点之间的最短路径。例如，4-1 的最短路径为 4-3-2-1。

弗洛伊德算法的具体实现

用弗洛伊德算法查找图 1 中各顶点之间最短路径的 Java 程序：

public class Floyd {
    static int V = 4; // 顶点的个数
    static int[][] P = new int[V][V]; // 记录各个顶点之间的最短路径
    static int INF = 65535; // 设置一个最大值
    // 中序递归输出各个顶点之间最短路径的具体线路
    public static void printPath(int i, int j) {
        int k = P[i][j];
        if (k == 0)
            return;
        printPath(i, k);
        System.out.print((k + 1) + "-");
        printPath(k, j);
    }
    // 输出各个顶点之间的最短路径
    public static void printMatrix(int[][] graph) {
        for (int i = 0; i < V; i++) {
            for (int j = 0; j < V; j++) {
                if (j == i) {
                    continue;
                }
                System.out.print((i + 1) + " - " + (j + 1) + "：最短路径为:");
                if (graph[i][j] == INF)
                    System.out.println("INF");
                else {
                    System.out.print(graph[i][j]);
                    System.out.print("，依次经过：" + (i + 1) + "-");
                    // 调用递归函数
                    printPath(i, j);
                    System.out.println((j + 1));
                }
            }
        }
    }
    // 实现弗洛伊德算法,graph[][V] 为有向加权图
    public static void floydWarshall(int[][] graph) {
        int i, j, k;
        // 遍历每个顶点，将其作为其它顶点之间的中间顶点，更新 graph 数组
        for (k = 0; k < V; k++) {
            for (i = 0; i < V; i++) {
                for (j = 0; j < V; j++) {
                    // 如果新的路径比之前记录的更短，则更新 graph 数组
                    if (graph[i][k] + graph[k][j] < graph[i][j]) {
                        graph[i][j] = graph[i][k] + graph[k][j];
                        // 记录此路径
                        P[i][j] = k;
                    }
                }
            }
        }
        // 输出各个顶点之间的最短路径
        printMatrix(graph);
    }
    public static void main(String[] args) {
        // 有向加权图中各个顶点之间的路径信息
        int[][] graph = new int[][] { { 0, 3, INF, 5 }, { 2, 0, INF, 4 }, { INF, 1, 0, INF }, { INF, INF, 2, 0 } };
        floydWarshall(graph);
    }
}

用弗洛伊德算法查找图 1 中各顶点之间最短路径的 Python 程序：

V = 4   # 顶点的个数
INF = 65535    # 设定一个最大值
P = [[0]*V for i in range(V)] # 记录各个顶点之间的最短路径
# 有向加权图中各个顶点之间的路径信息
graph = [[0, 3, INF, 5],
         [2, 0, INF, 4],
         [INF, 1, 0, INF],
         [INF, INF, 2, 0]]
# 中序递归输出各个顶点之间最短路径的具体线路
def printPath(i,j):
    k = P[i][j]
    if k == 0:
        return;
    printPath(i , k)
    print("%d-" % (k + 1) , end='')
    printPath(k , j)
# 输出各个顶点之间的最短路径
def printMatrix(graph):
    for i in range(V):
        for j in range(V):
            if j == i:
                continue
            print("%d - %d: 最短路径为:"%(i + 1, j + 1) , end='')
            if graph[i][j] == INF:
                print("INF")
            else:
                print(graph[i][j] , end='')
                print("，依次经过：%d-"%(i+1) , end='')
                # 调用递归函数
                printPath(i , j)
                print(j + 1)
# 实现弗洛伊德算法,graph[][V] 为有向加权图
def floydWarshall(graph):
    # 遍历每个顶点，将其作为其它顶点之间的中间顶点，更新 graph 数组
    for k in range(V):
        for i in range(V):
            for j in range(V):
                # 如果新的路径比之前记录的更短，则更新 graph 数组
                if graph[i][k] + graph[k][j] < graph[i][j]:
                    graph[i][j] = graph[i][k] + graph[k][j]
                    # 记录此路径
                    P[i][j] = k
    # 输出各个顶点之间的最短路径
    printMatrix(graph)
floydWarshall(graph)

以上程序的输出结果均为：

1 - 2: 最短路径为:3，依次经过：1-2
1 - 3: 最短路径为:7，依次经过：1-4-3
1 - 4: 最短路径为:5，依次经过：1-4
2 - 1: 最短路径为:2，依次经过：2-1
2 - 3: 最短路径为:6，依次经过：2-4-3
2 - 4: 最短路径为:4，依次经过：2-4
3 - 1: 最短路径为:3，依次经过：3-2-1
3 - 2: 最短路径为:1，依次经过：3-2
3 - 4: 最短路径为:5，依次经过：3-2-4
4 - 1: 最短路径为:5，依次经过：4-3-2-1
4 - 2: 最短路径为:3，依次经过：4-3-2
4 - 3: 最短路径为:2，依次经过：4-3